Let’s start with a small thought experiment: You are a semi-competitive and value-oriented Magic player. You just arrived at the site of the Grand Prix located near your home town. Due to your new job as an arctic explorer you rarely find time to play any bigger Magic events these days. It’s Friday and since you have no byes for the GP you are eager to play some trials. Surprisingly, Wizards Organized Play restructered the usual side event schedule. You find the following offer: “One player Trial — $35 — winner receives two byes”. In other words, you have the opportunity to buy two byes for just 35 dollar. Would you take it?

Figure 1: Copyright owned by Wizards of the Coast
This question adresses a few interesting aspects. Do you actually want to pass on playing two matches of tournament Magic? Would you pay money to increase your chances for a top8 result and associated fame and reputation? Here however, I’m solely interested in the pure equity aspect of this deal. Do you actually receive a corresponding increase of expected cash prize for your investment of 35 dollar? This post’s main question is:
Given a certain score during a Grand Prix or Pro Tour, what are your expected tournament winnings (EV)?
Frank Karsten already adressed this topic by calculating the expected cash prize for GPs and PTs. I really appreciate his straightforward approach using a binomial distribution for the final score. What bugged me, however, was the simplifying assumption of a stationary win probability throughout the tournament. In my last post, I argued that the win probability is in fact subject of variation due to different opponent skills in the various score brackets. Moreover, we even derived a model to estimate those win probabilities which I want to apply to our problem at hand.
Secondly, Frank Karsten only computes the expected payout prior to the event. Here I want to take a look at how these numbers change mid-tournament depending on your score. For instance, is your EV higher at a score of 5-1 or at 7-2? Finally, I will present a web application, which can be used to compute your EV on the fly (you should scroll down if thats all what you want to see).
WPT based score distributions
In order to compute the expected winnings within a tournament we need two things. Firstly, we need to know how likely is each possible final tournament score. Secondly, we need information on what payout is associated with each of those scores. Combining these, we can compute the average, i.e. the expected, payout. In this section we focus on the final score distribution.
In my last post I introduced the win probability tree (WPT), which – for a player with a certain skill – assigned a win probability to each possible score bracket within a GP. Skill was thereby defined as a specific rating according to MTGELOPROJECT. For our purposes, the distribution of the final tournament score of the player can be directly derived from his WPT.
To do so, we again denote by \(p_w^{(j)}(x)\) the probability of winning a match within the score bracket “w wins after j rounds” given your rating of \(x\). For instance, \(p_1^{(2)}(x)\) refers to the probability of winning your third round, if you have one win after two rounds. We now denote by \(\pi_w^{(j)}(x)\) the probability of reaching the bracket “w wins after j rounds”. Thus, the vector \[\mathbf{\pi}^{(j)}(x) = \left( \pi_0^{(j)}(x), \ldots, \pi_j^{(j)}(x) \right)\] represents the distribution over the possible scores, i.e. number of wins, after round \(j\). Assuming, you start with no byes, then your initial score is zero wins after zero rounds, which corresponds to a score distribution of \[\mathbf{\pi}^{(0)}(x) = \left( 1 \right).\] The score distribution for the subsequent rounds can then be computed recursively via \[\pi_w^{(j)}(x) = \pi_w^{(j-1)}(x) \cdot (1-p_w^{(j-1)}(x)) + \pi_{w-1}^{(j-1)}(x) \cdot p_{w-1}^{(j-1)}(x).\] This formula for computing the probability of having \(w\) wins after \(j\) rounds looks only at the two possibilities, that you either already had \(w\) wins after the previous rounds and lose the \(j\)-th match or you had \(w-1\) wins and win the \(j\)-th match. For the two special cases of having either only wins (\(\pi_j^{(j)}(x)\)) or having no wins (\(\pi_0^{(j)}(x)\)) one of the two terms must be omitted accordingly. This recursive formula must be applied to compute every possible score for each round up to the final round of the tournament, e.g. for all 15 rounds within a GP.
Note, that if the tournament has a day 2 cut requiring \(w^*\) wins after \(j^*\) rounds, we have to set the win probability \(p_w^{(j)}(x) = 0\) if \(w < w^*\) and \(j \geq j^*\), as it is rather unlikely to win any more matches if you haven’t made the cut.
The same procedure can be applied if we are interested in the final score distribution from a certain point during the tournament, e.g. from a score of 5-1. We just have to use a different initial distribution. Using the score of 5-1 as an example, we would have to set \[\mathbf{\pi}^{(6)}(x) = \left(0, 0, 0, 0, 0, 1, 0 \right),\] such that the bracket “5 wins after 6 rounds” is assigned a probability of 100%. The subseqent score distributions for the following rounds could then again be computed recursively starting with this “distribution”.
The biggest difference of applying the WPT based probabilities instead of assuming a stationary match win probability is that the resulting distribution is somewhat self-correcting. This is a consequence of the dynamic behaviour of match win probabilities within the WPT, which decrease after every match win and increase again after every loss. Thus, the final score distribution is a little under-dispersed, meaning that is has less variance than the simpler binomial distribution. Furthermore, the probability for achieving high scores of X-1 or X-2 is generally smaller, since the match win probability shrinks on the way to get there.
Score-associated payouts
Unfortunately, Knowing your final score does not tell you much about the money you win. For GPs and PTs the awarded prize money is tied to your rank in the final standings, which could be within a very wide range for most scores. Moreover, the range of, e.g., 12-3 players in the final standings of a GP depends on the total number of players and their number of byes. In this section I explain how to derive the expected payout for a given final score.
The approach is basically the same as Frank Karsten used to compute the expected payouts. For a given number of players \(n\) and given number of byes \(b_i\), (\(i=1,2,3\)) within the first, second and third round, respectively, I first compute the final standings of the corresponding tournament, i.e. for a GP scenario I compute how many players play 15-0, how many play 14-1, and so on. To do so, I apply a similar algorithm as presented in my previous post, which works as follows:
All \(n\) players start with a score of zero wins.
For each round repeat steps 3) to 5).
Sort the players by score.
The first \(b_i\) players receive byes, with \(i\) being the round number.
The remaining players are paired by order of current standings, with the first player of each pairing receiving the match win.
Make a final sort of the players by final score.
The result of this procedure is a sorted list of all tournament players combined with their respective final scores. This list can then be used to derive the range of each score within the final standings. Thus, for a final number of wins \(w\) let \(h_w\) and \(l_w\) denote the highest (worst) and lowest (best) rank among players with \(w\) wins within the standings. Let \(y_r\) be the prize money that is associated with rank \(r\). Then the average prize money \(m_w\) awarded to a player with \(w\) wins can be calculated by \[m_w = \frac{1}{1+h_w-l_w}\sum_{r=l_w}^{h_w} y_r,\] which is just the total money awarded to players with \(w\) wins devided by the number of these players.

Figure 2: Copyright owned by Wizards of the Coast
The biggest flaw of this appraoch is that it doesn’t account for potential draws during the tournament, wether intentional or not. However, it is still possible to roughly incorporate draws for EV calculation, for instance if you are interested in the EV of a 3-1-1 score. This will be adressed later. Another limitation is that I don’t account for potential prize money and fundings associated with awarded PT invitations.
Now let our powers combine! In order to compute the expected prize money payout \(m(x)\) for a certain player with rating \(x\) we can now just link this players final score distribution \(\mathbf{\pi}^{(j)}(x)\) with the score-associated payouts \(m_w\), i.e. for a GP we have \[m(x) = \sum_{w=0}^{15} \pi_w^{(15)}(x) \cdot m_w.\]
Average Joe’s EV
To provide an example, let’s look at the prize money EV for an average player (Joe) within a 1500 player GP. Joe has a match win percentage of 50% against the overall GP field, which corresponds to an MTGELOPROJECT rating of 1554. For each possible score I computed Joe’ prize money EV, which are shown in the figure below. For this example I used the WPT according to the normal player density as described in my last post.
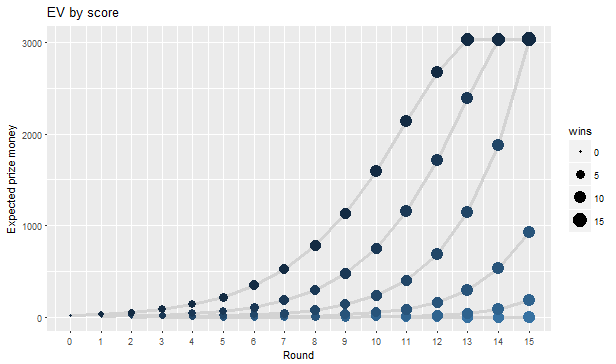
Figure 3: Expected prize money by score for an average GP player. Grey lines connect scores with the same number of losses, i.e. the highest line marks the X-0 scores, the next line marks the X-1 scores, and so on.
Joe’s initial EV when starting the tournament is 12.79 $. After a perfect day 1 – at a score of 9-0 – Joe’s EV would have increased to 881,74 $. By looking at the Figure above it is clear that the biggest jumps in EV occur in the later rounds at the higher scores of, e.g., X-1 and X-2. Incidently, the biggest EV gap is between the scores 13-2 and 12-3, which usually marks the difference of making Top8 or not. Coming back to our initial thought experiment: if Joe would be able to buy two byes for this event, he could increase his EV from 12.79 $ to 34.57 $, which wouldn’t be worth the hypothetical investment of 35 dollar. My personal conclusion: play Chaos Drafts instead of Trials.
Expected number of playmats
Using the same approach, it is also possible to compute the top8 chance associated with every possible score during the tournament. To do so, instead of looking at the awarded prize money, we look at the number of awarded Top8 playmats, i.e. the first eight players each receive one while all other players go home empty handed. Your top8 chance is then equivalent to the expected number of playmats you win.
The EV-Calculator
If you are interested in calculating your own EV during your upcoming tournament, may I present you the MTG-GP/PT-EV-Calculator, to be found here:
[https://mtganalyze.shinyapps.io/evcalculator/]
The calculator applies the model described above and calculates your expected winnings for a small variety of settings. In order to use it, you have to select the tournament type, GP or PT, your win rate against the player field and your current score. The EV-Calculator then shows you the following results:
Your current Tournament EV in the form of money, Pro Points, and your Top8 Chance
The amounts of Money, Pro Points, and Top8 Chance, that are at stake in your next match (i.e what is the difference in expected prize money if you win your next round compared to a loss in the next round)
The MTGELORATING matching your win percentage against the field (this is useful for accurately setting you win percentage)
Your corresponding WPT
In order to compute these results, the calculator makes some assumptions I haven’t discussed so far. These are:
TOP8 prizes: To compute your expected winnings in the case of making top8, the calculator computes your average win percentage against potential top8 players based on the simulatd standings and your WPT. This win probability is applied to every elimination round in order to compute your expected top8 payout.
Draws: Since draws were not possible in the simulated final tournament standings, it is not directly possible to derive were certain scores including draws would lead you. To still get a rough prediction, the calculator does the following. Three draws are transformed to one win and two losses. In the case of one or two draws, the calculator treats these as a loss, but instead of looking on the average payout associated with your final score, the calculator takes only the best payout matching your final score. Thus, for instance the prize money associated with a score of 12-2-1 is equal to the highest possible prize money of any 12-3 player.
Byes: In order to simulate the final standings, the calculator needs input data on how many byes are awarded in the first three rounds. To get these numbers I looked at four recent GPs (Turin, Washington DC, Metz, Indianapolis all 2017) and searched for the corresponding fraction of players with one, two, and three byes. I computed the average of these fractions, to obtain the following input: 42.4 % of players receive round one byes, 26.5 % receive byes for round two and a 1.9 % of all players receive three byes.
End of turn
I compured the calculator results with some of the numbers derived by Frank Karsten. For instance in a 900 person GP at zero byes and a win percentage of 60%, the calculator computes an expected prize money of 142 $ whereas Frank Karsten arrives at 155 $. The calculator generally computes slightly lower results, since according to the underlying model the win probabilities within the relevant score brackets are even smaller compared to the overall win percentage, while Frank Karsten’s model does not make this adjustment.
What I also found to be very interesting that the amount of money at stake in the next round is most often larger than your current expected winning. Thus, you somewhat play double-or-nothing during your whole tournament life.

Figure 4: Copyright owned by Wizards of the Coast
Lastly, I would again appreciate your feedback. Would you wish to obtain some further information from the MTG-GP/PT-EV-Calculator? If so, what are you interested in? Could you imagine to use the calculator during a tournament, maybe for motivational reasons? Please, let me hear your opinion.